python_最小二乗法　least-squares analysis（その2）

前回の続きです。次は解析解で解いてみましょう。

直線の式、ｙ＝ax+b、　　　i 番目の点の座標を(xi,yi)とすると、

i番目の点と直線の距離は、　m=(ｙi-(axi+b))2とします。

これの∑をとって、それを最小にします。

その2　解析解

要するに、a やbをを変化させたときに極小にｍがいればよい。すなわち、極小なら傾きが０なので、

aで微分が０

\(\frac{δm}{δa}=\Sigma (2ax^2-2xy+2bx) =0\)

すなわち、

\(\frac{δm}{δa}=2a\Sigma x^2-2\Sigma xy+2b\Sigma x=0\)—①

同様にbでの微分が０

\(\frac{δm}{δb}=2b\Sigma -2\Sigma y+2a\Sigma x=0\)—②

①と②より、a,bを解くと

\(a=\frac{\Sigma xy*\Sigma -\Sigma y} {\Sigma x^2 *\Sigma -\Sigma x}\)

\(b=\frac{\Sigma y -a*\Sigma x} {\Sigma }\)

これで求まる直線の式、ｙ＝ax+b　が最小二乗法の式になります。

解析解は求まると、コードも楽ですね。

import matplotlib.pyplot as plt
import numpy as np

vx=np.array([2,4,6,8,5,2])
vy=np.array([3,4,7,8,7,5])

s1=len(vx)
sx=sum(vx)
sxx=np.dot(vx,vx)#ベクトル内積
sxy=np.dot(vx,vy)#ベクトル内積
sy=sum(vy)

aa=(sxy*s1-sy)/(sxx*s1-sx)
bb=(sy-sx*aa)/s1
print("y=",aa,"x+",bb)

#-------------------------------------
#ここからグラフ化
plt.figure(dpi=150)
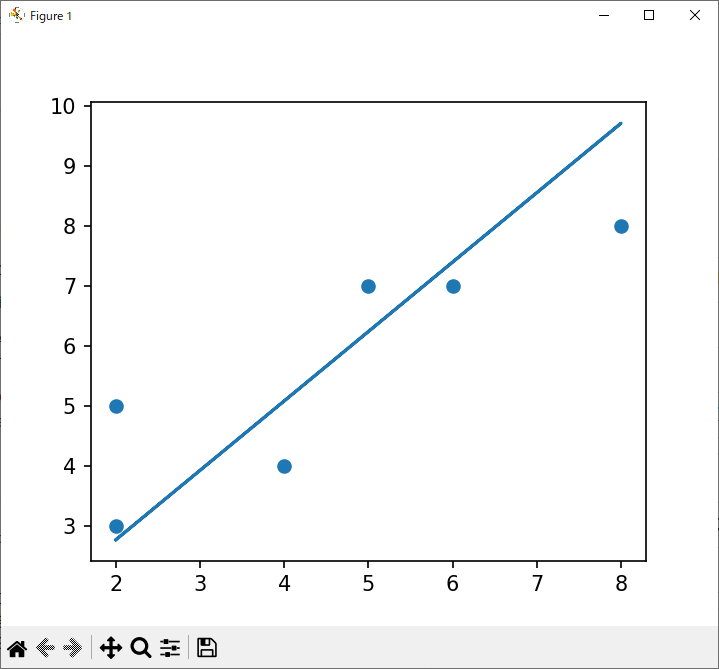
plt.scatter(vx,vy)
y_line=[]
for xi in vx:
    y_line.append(aa*xi+bb)
plt.plot(vx,y_line)
plt.show()